Oferecido por
O cientista da computação Marijn Heule está sempre em busca de um bom desafio matemático. Professor associado da Carnegie Mellon University, Heule tem uma reputação impressionante por resolver problemas matemáticos intratáveis com ferramentas computacionais. Seu resultado de 2016 com o “problema booliano dos trios pitagóricos” foi uma prova tremenda que ganhou as manchetes: “A prova de resolução matemática de duzentos terabytes é a maior de todos os tempos”. Ele está atualmente implementando uma abordagem automatizada para lidar com a conjectura simples e cativante de Collatz.
Proposto pela primeira vez (de acordo com alguns relatos) na década de 1930 pelo matemático alemão Lothar Collatz, este problema de teoria dos números fornece uma receita, ou algoritmo, para gerar uma sequência numérica: comece com qualquer número inteiro positivo. Se o número for par, divida por dois. Se o número for ímpar, multiplique por três e some um. E então faça o mesmo, de novo e de novo. A conjectura garante que a sequência sempre terminará em 1 (e, em seguida, passará continuamente por 4, 2, 1).
O número 5, por exemplo, gera apenas seis termos:
5, 16, 8, 4, 2, 1
O número 27 passa por 111 ciclos, oscilando para cima e para baixo, e seu número mais alto chega a 9.232, antes de finalmente terminar em 1.
O número 40 gera outra breve sequência:
40, 20, 10, 5, 16, 8, 4, 2, 1
Até o momento, a conjectura foi verificada por computador para todos os valores iniciais até quase 300 trilhões, com cada número eventualmente terminando em 1.
A maioria dos pesquisadores acredita que a conjectura é verdadeira. Atraiu multidões de matemáticos e não matemáticos, mas ninguém produziu uma prova. No início dos anos 1980, o matemático húngaro Paul Erdős declarou: “A matemática ainda não está pronta para esses problemas”.
“O que queremos saber é se humanos ou computadores são melhores para resolver esses problemas”. Marijn Heule
“E ele provavelmente está certo”, diz Heule. Para ele, o apelo de Collatz não é tanto o potencial de avanço, mas o avanço das técnicas de raciocínio automatizado. Depois de estudá-lo por cinco anos, Heule e seus colaboradores, Scott Aaronson e Emre Yolcu, postaram recentemente um artigo no servidor de pré-impressão, arXiv. “Embora não tenhamos conseguido provar a conjectura de Collatz”, eles escrevem, “acreditamos que essas ideias representam uma nova abordagem interessante”.
“É um nobre fracasso”, diz Aaronson, um cientista da computação da Universidade do Texas em Austin. Um fracasso porque eles não provaram a conjectura. Nobre porque eles fizeram progresso em outro sentido: Heule vê isso como um ponto de partida para determinar se humanos ou computadores são melhores em resolver tais problemas.
Traduzindo matemática para computação
Para muitos problemas matemáticos, os computadores são inúteis, uma vez que não têm acesso à vasta obra de matemática acumulada ao longo da história. Mas às vezes os computadores se sobressaem onde os humanos não têm esperança. Diga a um computador a aparência de uma solução – dê a ele um objetivo e um espaço de busca bem definido – e então, com força bruta, o computador poderá encontrá-la. No entanto, esta é uma questão de debate, isto é, se os resultados computacionais equivalem a adições significativas ao cânone matemático. A opinião tradicional é que apenas a criatividade e a intuição humanas, por meio de conceitos e ideias, ampliam o escopo da matemática, enquanto os avanços por meio da ciência da computação são frequentemente descartados como engenharia.
Em certo sentido, o computador e a conjectura de Collatz são uma combinação perfeita. Por um lado, como aponta Jeremy Avigad, especialista em lógica e professor de filosofia da Carnegie Mellon University, a noção de um algoritmo iterativo está no cerne da ciência da computação, e as sequências de Collatz são um exemplo de um algoritmo iterativo, procedendo gradualmente de acordo com uma determinada regra. Da mesma forma, mostrar que um processo termina é um problema comum na computação. “Os cientistas da computação geralmente querem saber se seus algoritmos estão concluídos, isto é, se eles sempre dão uma resposta”, enfatiza Avigad. Heule e seus colaboradores estão aproveitando essa tecnologia para lidar com a conjectura de Collatz, que na verdade é apenas um problema de terminação.
“A beleza desse método automatizado é que você pode ligar o computador e esperar.” Jeffrey Lagarias
A especialidade de Heule é com uma ferramenta computacional chamada de “solucionador SAT”, ou “satisfatibilidade”, um programa de computador que determina se há uma solução para uma fórmula ou problema dado um conjunto de restrições. O que é crucial, no caso de um desafio matemático, é que o solucionador SAT primeiro precisa do problema traduzido, ou representado, em termos que o computador possa entender. E como Yolcu, aluno de doutorado de Heule, enfatiza: “A representação importa muito”.
Uma aposta arriscada, mas vale a pena tentar
Quando Heule mencionou pela primeira vez lidar com Collatz com um solucionador SAT, Aaronson pensou: “Não há nenhuma maneira de isso funcionar”. Mas ele se convenceu facilmente de que valia a pena tentar, pois Heule descobriu algumas maneiras sutis de tornar esse antigo problema mais flexível. Ele notou que uma comunidade de cientistas da computação estava usando solucionadores SAT para encontrar provas de conclusão para uma representação abstrata de computação chamada de “sistema de reescrita”. Foi um tiro no escuro, mas ele sugeriu a Aaronson que transformar a conjectura de Collatz em um sistema de reescrita poderia tornar possível obter uma prova de terminação para ele (Aaronson já havia ajudado a transformar a hipótese de Riemann em um sistema computacional, codificando-a em uma pequena máquina de Turing). Naquela noite, Aaronson projetou o sistema. “Era como um dever de casa, um exercício divertido”, diz ele.
“Em um sentido muito literal, eu estava lutando contra um Terminator, ou pelo menos, um demonstrador do teorema da terminação”. Scott Aaronson
O sistema de Aaronson registrou o problema de Collatz com 11 regras. Se os pesquisadores pudessem obter uma prova de conclusão para esse sistema análogo, aplicando essas 11 regras em qualquer ordem, isso provaria que a conjectura de Collatz é verdadeira.
Heule o testou com ferramentas de última geração para provar a terminação de sistemas de reescrita, o que não funcionou; foi decepcionante e surpreendente. “Essas ferramentas são otimizadas para problemas que podem ser resolvidos em um minuto, enquanto qualquer abordagem para resolver Collatz provavelmente requer dias, senão anos de computação”, diz Heule. Isso forneceu motivação para aprimorar sua abordagem e implementar suas próprias ferramentas para transformar o problema de reescrita em um problema SAT.
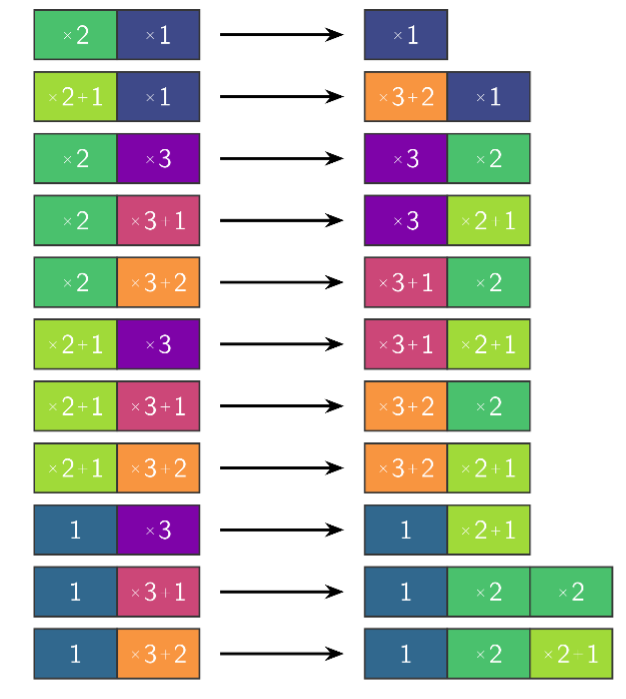
Uma representação do sistema de reescrita de 11 regras para a conjectura de Collatz. MARIJN HEULE
Aaronson achou que seria muito mais fácil resolver o sistema de 11 regras com uma a menos, criando assim um sistema “semelhante ao de Collatz”, um teste decisivo para o objetivo maior. Ele lançou um desafio de pessoas contra computadores: o primeiro a resolver todos os subsistemas com 10 regras vencidas. Aaronson experimentou manualmente. Heule o testou com o solucionador SAT: ele codificou o sistema como um problema de satisfatibilidade, com outra camada inteligente de representação, traduzindo o sistema no jargão de variáveis de computador que podem ser 0 e 1, e então deixou seu solucionador SAT rodar nos núcleos, procurando prova de terminação.
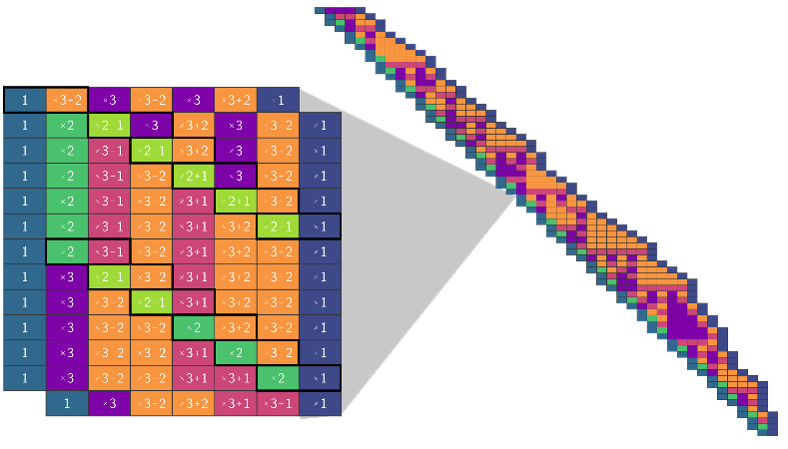
O sistema segue a sequência de Collatz para o valor inicial 27 (27 está no canto superior esquerdo da cascata diagonal, 1 está no canto inferior direito). Existem 71 etapas, em vez de 111, pois os pesquisadores usaram uma versão diferente, mas equivalente do algoritmo de Collatz: se o número for par, divida por 2; caso contrário, multiplique por 3, some 1 e, em seguida, divida o resultado por 2. MARIJN HEULE
Ambos conseguiram provar que o sistema termina com os vários conjuntos de 10 regras. Às vezes, era uma tarefa trivial, tanto para o ser humano quanto para o programa. A abordagem automatizada de Heule levou no máximo 24 horas. A abordagem de Aaronson exigiu um esforço intelectual significativo, demorando algumas horas ou mesmo um dia – um conjunto de dez regras que ele nunca conseguiu provar, embora acredite com muita convicção que poderia fazê-lo, com mais esforço. “Em um sentido muito literal, eu estava lutando contra um Terminator” Aaronson diz, “ou pelo menos, um demonstrador do teorema da terminação”.
Desde então, Yolcu ajustou o solucionador SAT, calibrando a ferramenta para melhor se adequar à natureza do problema de Collatz. Esses truques fizeram toda a diferença, acelerando as provas de terminação para os subsistemas de 10 regras e reduzindo os tempos de execução a meros segundos.
“A principal questão que permanece”, explica Aaronson, “seria: e quanto ao conjunto completo de 11 regras? Se tentarmos executar o sistema no conjunto completo, ele nunca termina, o que talvez não deva nos surpreender, porque este é o problema de Collatz”.
Na opinião de Heule, a maioria das pesquisas em raciocínio automatizado ignora os problemas que exigem muita computação. Mas, com base em suas descobertas anteriores, ele acredita que esses problemas podem ser resolvidos. Outros transformaram o problema de Collatz em um sistema de reescrita, mas é a estratégia de usar um solucionador SAT ajustado com um incrível poder de computação que poderia ganhar força em direção a uma prova.
Até agora, Heule realizou a pesquisa de Collatz usando cerca de 5.000 núcleos (as unidades de processamento que alimentam os computadores; os computadores convencionais de consumidores têm quatro ou oito núcleos). Como um Amazon Scholar, você tem um convite aberto da Amazon Web Services para acessar recursos “virtualmente ilimitados”, de até um milhão de núcleos. Mas Heule reluta em usar números maiores.
“Eu quero alguma indicação de que esta é uma tentativa realista”, diz ele. Caso contrário, Heule sente que estará desperdiçando recursos e confiança. “Não preciso de uma garantia de 100%, mas a verdade é que gostaria de ter algumas evidências de que existe uma probabilidade razoável de que serei bem-sucedido”.
Turbinando uma transformação
“A beleza desse método automatizado é que você pode ligar o computador e esperar”, diz o matemático Jeffrey Lagarias, da Universidade de Michigan. Ele brincou com Collatz por cerca de cinquenta anos e se tornou o detentor do conhecimento, compilando bibliografias de suas anotações e editando um livro sobre o assunto, “The Ultimate Challenge”. Para Lagarias, a abordagem automatizada trouxe à mente um artigo de 2013 do matemático de Princeton, John Horton Conway, que refletiu que o problema de Collatz pode estar entre uma classe elusiva de problemas que são verdadeiros e “indecidíveis”, mas ao mesmo tempo não demonstravelmente indecidíveis. Como Conway apontou, “pode até ser que a afirmação de que eles não são prováveis não seja provável, e assim por diante”.
“Se Conway estiver certo”, diz Lagarias, “não haverá prova, automatizada ou não, e nunca saberemos a resposta”.
A pessoa que possivelmente chegou mais perto de uma solução é o matemático Terence Tao, da Universidade da Califórnia, Los Angeles. Em 2019, Tao provou que a conjectura de Collatz é “quase” verdadeira para “quase” todos os números (“quase” depende de duas definições técnicas diferentes).
Tao acredita que uma prova humana da conjectura seria mais matematicamente significativa (para entender o porquê) do que uma prova computacional. “Mas o fato de um grande problema não resolvido recair sobre um programa automatizado pode levar a uma transformação revolucionária na maneira como os matemáticos usam a assistência do computador em seu trabalho”, diz ele. “Com um problema tão insolúvel como este, aceitaremos todo o conhecimento que pudermos obter”.
O que Heule e seus colaboradores realmente querem, no entanto, é um cenário tal que – usando essa abordagem, com esse problema – o computador tenha sucesso onde o humano falha, ou vice-versa. “Neste ponto, não sabemos se essas técnicas são muito melhores do que as usadas manualmente pelas pessoas ou não, ou se os humanos podem fazer coisas que o computador não pode”, conclui Heule. “O que queremos saber é se as pessoas ou os computadores são melhores para resolver esse tipo de problema”.
Para esse fim, vamos ver quem resolve a conjectura de Collatz primeiro.